![]()
ГРАВИТАЦИЯ
«ЭЛЕКТРОМАГНИТНАЯ»
2. 1. Магнитные свойства вещества
Магнетизм является универсальным свойством материи и обнаруживается во всем окружающем нас мире – от микрочастиц до космических объектов. Рассматривая далее «гравитационную медаль» с позиций этого явления, попытаемся увязать такие понятия как гравитация и магнетизм на простой основе. Представим себе, что Земля и какой-то физический объект, покоящийся на ее поверхности, например, знакомый уже нам монолитный куб каменной соли (NaCl), притягиваются друг к другу как два магнита соответствующих размеров (рис.12).
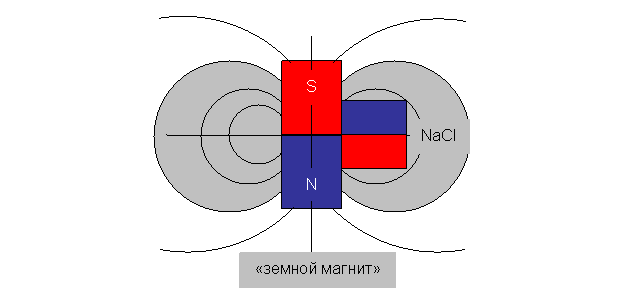
Рис.12
В отношении Земли особенно напрягать свое воображение не нужно. Она по существу и является огромным магнитом. В первом приближении магнитное поле Земли подобно полю гигантского магнитного диполя, расположенного в центральных частях земного шара, с Южным магнитным полюсом в северном полушарии и с Северным магнитным полюсом в южном полушарии Земли. Магнитный момент (РМ Z ) этого диполя (здесь – произведение намагниченности на объем магнита) примерно равен 8*1015 А * м2 [5].
Примечание
3: впервые идея о том, что наша планета
представляет собой «большой магнит», была сформулирована английским врачом
и физиком Уильямом Гильбертом
в 1600 году.
С учетом всех особенностей глобального магнитного поля Земли наибольшая его индукция В = 6,8*10-5 Тл (тесла) достигается вблизи Северного магнитного полюса (в Антарктиде), наименьшая В = 2,4*10–5 Тл – в Бразилии.
Таким образом, некоторые представления о «большом магните» у нас имеются. Остается выявить магнитные качества второго объекта – монолитного куба каменной соли единичного объема, которые могли бы обеспечить его притяжение к земной поверхности с силой, равной весу этого тела. Но для этого придется кое-что вспомнить о магнитных свойствах вещества.
Причина, вследствие которой вещества обладают магнитными свойствами, была впервые найдена французским ученым Андре Мари Ампером.

Андре Мари Ампер (1775 – 1836)
Сначала,
наблюдая в опытах Эрстеда магнитную стрелку, которая отклонялась вблизи
проводника с током, Ампер предположил, что магнетизм Земли вызван токами,
текущими внутри земного шара. Главный шаг был сделан: магнитные свойства тела
можно объяснить циркулирующими внутри его токами. Далее Ампер пришел к общему
заключению: магнитные свойства любого тела определяются замкнутыми электрическими
токами внутри него.
Итак, согласно гипотезе Ампера, справедливость которой уже доказана прямыми экспериментами, внутри молекул и атомов циркулируют элементарные электрические токи, которые проявляются в виде магнитных свойств вещества.
И действительно, каждый атом может быть уподоблен замкнутому электрическому току I, текущему по плоскому контуру с площадью S (атомный ток). Получается некая микропетля с током (рис.13). А петли с током, или магнитные диполи, не только создают магнитные поля, но и сами подвергаются действию силы, попав в стороннее магнитное поле. Если элементы замкнутого контура с током I лежат в плоскости, перпендикулярной направлению магнитного поля В, то и элементарные силы DF, действующие на отдельные участки контура, будут лежать в этой же плоскости. И если поле всюду однородное, то эти силы только деформируют контур (сжимают или растягивают его в зависимости от направления тока), а равнодействующая этих сил равна нулю (рис.14).
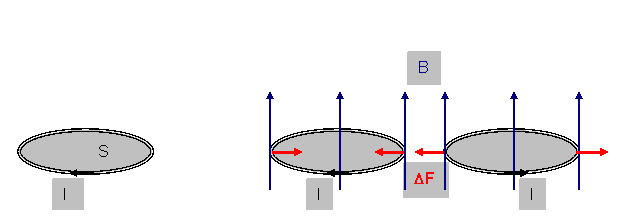
Рис.13 Рис.14
Если же поле неоднородное, то равнодействующая элементарных сил (FM) не равна нулю; контур не только деформируется, но и перемещается в ту область, куда направлена равнодействующая.
Рассчитаем эту равнодействующую для прямоугольной рамки с током I в неоднородном поле, в котором вектор В уменьшается вдоль оси ОХ по линейному закону так, что (рис.15):
![]() ,
(30)
,
(30)
где: DВ / Dх – средняя скорость изменения В вдоль оси ОХ.
Тогда F1 > F2 и разность
![]() ,
(31)
,
(31)
где: S = a b – площадь рамки. Условимся изображать контур с током некоторым вектором РМ, численно равным IS и направленным перпендикулярно плоскости контура в соответствии с правилом правого винта. Тогда:
![]() .
(32)
.
(32)
Если направление вектора РМ совпадает с направлением вектора В, то на контур действует сила, направленная в сторону возрастания В, т. е. контур будет втягиваться в поле. Если же направления векторов РМ и В не совпадают, то на контур действует сила, направленная в сторону убывания В, т. е. такой контур будет выталкиваться из поля.
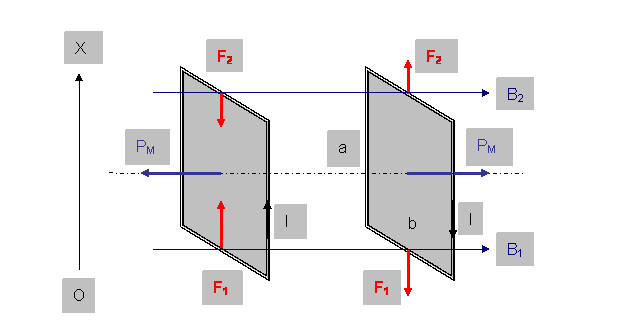
Рис.15
Полагая, что магнитное поле Земли воздействует на атомы вещества как на микроконтуры с током, вычислим магнитные моменты некоторых из них, а затем сделаем расчеты по определению магнитных моментов, которые должны быть в целом у физических объектов, интересующих нас в данной задаче.
Не вдаваясь особенно в тонкости теории магнетизма, здесь достаточно отметить, что в веществе число электронов равно числу протонов, а спиновый магнитный момент электрона почти в 2000 раз больше магнитного момента протона. Вполне очевидно, что именно электроны задают телам различной природы их основные магнитные свойства, к тому же эти свойства во многом зависят от распределения электронов в их оболочках.
Возьмем к примеру каменную соль (NaCl). Исследования оптических спектров щелочных металлов показали, что магнитный момент их атомного остатка (т. е. ядра и остальных электронов, кроме наименее связанного или «оптического» электрона, удаляющегося при ионизации) равен нулю. Следовательно, магнитный момент щелочного металла, в частности натрия, равен всего лишь моменту его оптического (валентного) электрона 3s1 (см. рис.7):
![]() ,
(33)
,
(33)
где: I = e / T – сила тока, вызванная движением валентного электрона в атоме, А (ампер);
е – заряд электрона, Кл;
Т – период обращения электрона по орбите, с.
Определим усредненные по времени (из-за прецессии) магнитные моменты атомов натрия (Р¢М Na) и хлора (Р¢M Cl). Для этого воспользуемся информацией, заложенной в термах указанных атомов.
Терм – это символ, в котором собраны нужные сведения о свойствах электронной конфигурации данного атома в его основном состоянии. Основным термом натрия является символ 2 S 1 / 2 , а термом хлора – 2 S 3 / 2 . Структура термов такова: латинская большая буква в них обозначает общий орбитальный момент (L) электронов атома со следующим соответствием:
при S, P, D, F, … и далее по алфавиту
L = 0, 1, 2, 3, … и т. д.
Нижний индекс терма показывает величину полного момента количества движения (J) электронной системы атома, а индекс наверху – число подуровней для данного значения L, равное 2 S + 1 (здесь S – полный спин электронов атома).
Примечание
4: квантовое число S не следует путать с символом терма – S.
Усредненный по времени магнитный момент любого атома определяется по формуле:
![]() ,
(34)
,
(34)
где: m В = 9,3*10-24 А * м2 – магнетон Бора (равен значению магнитного момента электрона);
![]() – множитель (фактор) Ланде. (35)
– множитель (фактор) Ланде. (35)
Так, для терма атома натрия (при J = 1 / 2, S = 1 / 2, L = 0) множитель Ланде равен:
![]() .
(36)
.
(36)
Отсюда, магнитный момент атома натрия (P/M Na), создаваемый одним его валентным электроном 3s1, в нормальном состоянии и усредненном значении примерно равен:
![]() А * м2. (37)
А * м2. (37)
Для терма атома хлора (при J = 3 / 2, S = 1 / 2, L = 1) множитель Ланде равен:
![]() .
(38)
.
(38)
Тогда магнитный момент атома хлора (Р/М Cl), создаваемый одним его некомпенсированным электроном подуровня 3р (см. рис.7), должен быть равным:
![]() А * м2. (39)
А * м2. (39)
А теперь, имея базовые величины магнитных моментов атомов натрия и хлора, найдем возможные значения магнитных моментов ионов Na+ и Cl- в поверхностном слое кристалла каменной соли.
Как мы помним из электростатического варианта подобного примера, при взаимодействии атомов Na и Cl более энергичный хлор оттягивает на себя около 80% электрического заряда от валентного электрона атома натрия. Если полагать, что в результате такого взаимодействия на 80% уменьшится и магнитный момент атома натрия [поскольку РМ = (е / Т)S], то его оставшаяся двадцатипроцентная часть и будет являться магнитным моментом иона натрия (Р/М Na+) в кристалле NaCl, то есть:
если 100 % – Р/М Na = 1,7*10-23 А * м2,
то 20 % – Р/М Na+ = 3,4*10-24 А * м2. (40)
В таком случае атом хлора, получивший «прибавку» в размере 80 % от заряда электрона своего партнера, превратится в ион Cl- с магнитным моментом (Р/М Cl-):
если 100 % – Р/М Cl- = 2,3*10-23 А * м2,
то 180 % – Р/М Cl- = 4,1*10-23 А * м2. (41)
В результате имеем значения магнитных моментов ионов натрия (40) и
хлора (41), составляющих поверхностный слой кристалла каменной соли.
Зададимся теперь вопросом: какой может быть пространственная ориентация двух соседних ионов натрия и хлора по отношению друг к другу в кристалле, если посмотреть на них как на элементарные источники магнитного поля или, проще говоря, микромагнитики?
Очевидно, наиболее целесообразным взаиморасположением двух соседних частиц было бы такое, при котором их атомные токи (i) в области сближения имели бы одинаковое направление (подобие двух соприкасающихся шестерен в механизме).

Рис.16
При этом векторы магнитных моментов данных ионов будут направлены в противоположные стороны (рис.16а).
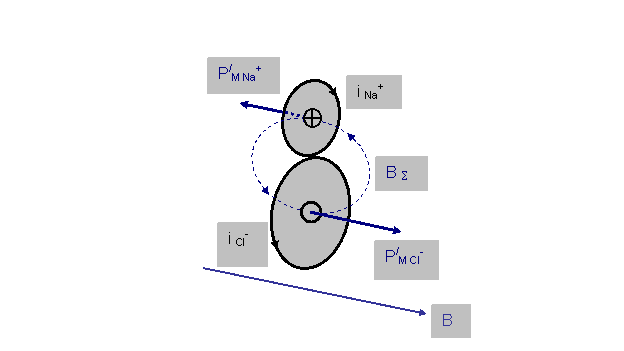
Рис.16а
Атомы, обладающие некоторым магнитным моментом РМ, называются парамагнитными. При внесении такого атома во внешнее магнитное поле его атомный ток стремится расположиться так, чтобы вектор РМ был ориентирован по направлению вектора В индукции внешнего поля и был ему параллелен.
Можно предположить, что в высокочастотном магнитном поле Земли преимущество в такой ориентации относительно вектора В этого поля в кристалле каменной соли будет иметь ион Cl-, поскольку его магнитный момент (РМ Cl-) почти в 12 раз больше магнитного момента (РМ Na+) иона натрия. Естественно, находясь в мощной сфере влияния атома хлора, атом натрия в кристалле NaCl вынужден будет обратить свой магнитный момент в противоположную сторону, чтобы при образовании кристалла их магнитные поля объединились в общее поле (ВS) для обеспечения взаимного притяжения атомов друг к другу с минимальными энергетическими затратами.
Если представить себе направления атомных токов в элементарной ячейке кристалла NaCl, то можно предположить, что эти токи на внутренних линиях схемы взаимно нейтрализуются. Некомпенсированными остаются противоположно направленные токи поверхностных ионов Na+ и Cl- (рис.17). Попробуем определить их значения и, вычислив разность, узнаем результирующую величину элементарного тока (Di) определенного направления на участке между двумя соседними ионами Na+ и Cl-.
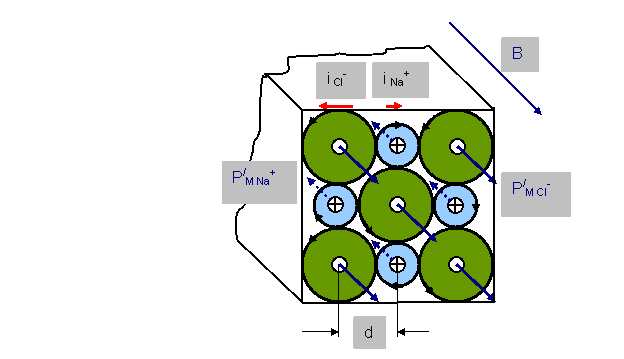
Рис.17
Известно, что радиус иона натрия в кристалле каменной соли равен r = 9,8*10-11 м [4]. Cледовательно, площадь (S r) его плоского электрического контура, ограниченного траекторией движения валентного электрона, примерно равна:
S r = p r2 = 3,14 (9,8*10-11)2 = 3*10-20 м2. (42)
Тогда сила тока в контуре иона натрия (i Na+) должна соответствовать величине:
![]() А.
(43)
А.
(43)
Радиус иона хлора R = 1,81*10-10 м. Значит площадь (S R) его контура составляет:
S R = p R2 = 3,14 (1,81*10-10)2 = 1*10-19 м2. (44)
Сила тока в электрическом контуре иона хлора (i Cl-) получается равной:
![]() А.
(45)
А.
(45)
Разность значений (Di) этих токов противоположного направления между двумя соседними ионами натрия и хлора на отрезке расстояния d = 2,79*1010 м составит:
![]() А.
(46)
А.
(46)
На отрезке длиной в 1 м суммарная величина таких токов (SDi) одного направления должна достигать:
![]() А.
(47)
А.
(47)
Замкнутый электрический контур в виде квадратной рамки с длиной ее стороны в 1 м и током I = SDi = 5,4*105 А имел бы магнитный момент (Р/М ), равный:
Р/М = I S = 5,4*105 * 1 = 5,4*105 А * м2. (48)
Если кристалл каменной соли кубической формы и единичного объема уподобить условной конструкции, состоящей из набора таких электрических рамок-контуров, то количество (n) этих контуров соответствовало бы числу ионов Na+ и Cl-, поместившихся на линии ребра данного куба (рис.18):
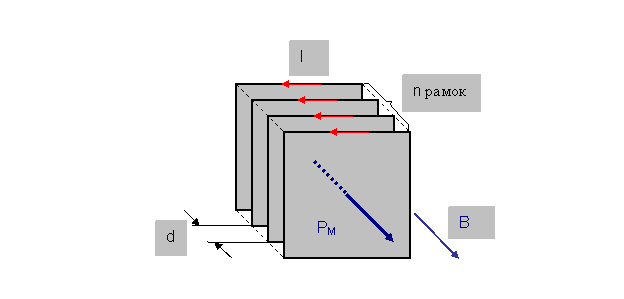
Рис.18
![]() рамок.
(49)
рамок.
(49)
И тогда общий магнитный момент (РМ) всех рамок, т. е. магнитный момент кристалла NaCl вышеуказанных размеров, получается равным:
РМ = Р/М * n = 5,4*105 * 3,6*109 = 1,9*1015 А * м2. (50)
Опуская предыдущие промежуточные выкладки, магнитный момент (РМ) условного кристалла каменной соли кубической формы и единичного объема можно выразить следующей формулой и ее числовым значением:
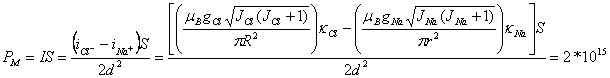 А * м2, (51)
А * м2, (51)
где: I – общая результирующая сила тока электронных оболочек поверхностных
ионов хлора (Cl-) и натрия (Na+) рассматриваемого
объекта;
S –
площадь сечения куба каменной соли (параллельно одной из его граней и
перпендикулярно силовым линиям магнитного поля В);
i Cl- – сила тока в электронной оболочке иона хлора (Cl-);
i Na+ - сила тока в оболочке иона
натрия (Na+);
d = 2,79*10-10 м –
константа кристаллической решетки каменной соли;
m В = 9,3*10-24
А * м2 – магнетон Бора;
g Cl = 1,3 – множитель (фактор)
Ланде для основного терма атома хлора (2 Р3 / 2);
g Na = 2 – множитель Ланде для
основного терма атома натрия (2 S1 / 2);
J Cl = 3 / 2 – квантовое число полного момента
количества движения атома хлора;
J Na = 1 / 2 – квантовое число
полного момента количества движения атома натрия;
R = 1,81*10-10 м –
эффективный радиус иона хлора (Cl-) в кристалле NaCl;
r = 9,8*10-11 м –
эффективный радиус иона натрия (Na+) в этом кристалле;
k Cl = 1,8; k Na = 0,2.
Примечание
5: в отношении
коэффициентов k Cl и k Na можно пояснить следующее. При взаимодействии
двух атомов (Na и Cl) с образованием из них связанной пары ионов (Na+
и Сl-) атом хлора
как бы «оттягивает» на себя согласно экспериментальным данным около 80 % облака валентного электрона атома натрия (с
орбитали 3s1). В результате этого валентный электрон атома натрия
лишается 0,8 элементарного электрического заряда. Поэтому в формуле (51)
поправочный коэффициент k Na
= (1 – 0,8) = 0,2. Соответственно, валентный электрон атома хлора
приобретает 0,8 части элементарного электрического заряда. Отсюда, коэффициент
k Cl = (1 + 0,8)
= 1,8.
______________________________
2. 2.
Динамическая модель механизма гравитации
В основу наших дальнейших рассуждений об электромагнитной природе земного притяжения положим формулу:
![]() ,
(52)
,
(52)
где: FM – сила электромагнитного притяжения физического тела к Земле, Н;
РМ – магнитный момент этого тела, А * м2;
DBZ / Dh – средняя скорость изменения индукции магнитного поля (BZ) Земли
по высоте (h) в слое до 1 м от ее уровенной поверхности, Тл / м.
Определим среднюю скорость изменения индукции магнитного поля Земли (DВZ / Dh) в каком-нибудь районе ее магнитного экватора. Будем считать, что в таком месте силовые линии магнитного поля в метровом слое от земной поверхности должны быть ей параллельны. «Взвешивание» наших объектов на геомагнитном экваторе позволит сократить и упростить дальнейшие расчеты.
Итак:
![]() ,
(53)
,
(53)
где:
![]() Тл,
(54) – величина индукции
магнитного поля Земли у ее поверхности
Тл,
(54) – величина индукции
магнитного поля Земли у ее поверхности
на геомагнитном экваторе в точке пересечения его с экватором географическим [2],
где: PM Z = 8*1015 А * м2 – магнитный момент земного диполя;
RZ = 6378140 м – расстояние от центра Земли до ее поверхности в районе географического экватора;
Ф = 0° – геомагнитная широта.
![]() Тл,
(55) – величина индукции магнитного
поля Земли
Тл,
(55) – величина индукции магнитного
поля Земли
на высоте h = 1 м от земной поверхности.
Примечание
6: ввиду того, что величины В¢Z
и В²Z в слое Dh = 1 м мало отличаются друг от друга,
результаты вычислений в формулах (54) и (55) представлены семью значащими
цифрами.
В итоге средняя скорость
изменения индукции магнитного поля Земли (DВZ / Dh) в районе геомагнитного
экватора в метровом слое от ее поверхности получается равной:
![]() Тл / м,
(56)
Тл / м,
(56)
а расчетная величина электромагнитной силы притяжения (FM) кубического кристалла каменной соли единичного объема примерно равна:
![]() Н.
(57)
Н.
(57)
В данном примере пришлось
сопрягать между собой физические параметры широкого диапазона (от микро- до
макровеличин) в приблизительных их значениях. Но, думается, что разница между
полученными значениями веса Р = 2,12*104 Н и сил: FE = – 2,1*104 Н, FM = 2*104 Н – невелика. Ее можно считать вполне приемлемой.
В целях экономии времени и
печатной площади раздел 2.1. завершим рассмотрением магнитных свойств объекта
из алюминия. Но предварительно обсудим некоторые представления о внутренней
структуре веществ и их модельные отображения в кристаллографии.
В области структурной кристаллографии созданы различные модели «упаковки» атомов в кристаллах. Чаще всего роль атомов (ионов) в узлах их решеток играют шары. Так, например, структура кристалла каменной соли имитируется шарами разного диаметра в соответствии с размерами ионов натрия и хлора (рис.19).
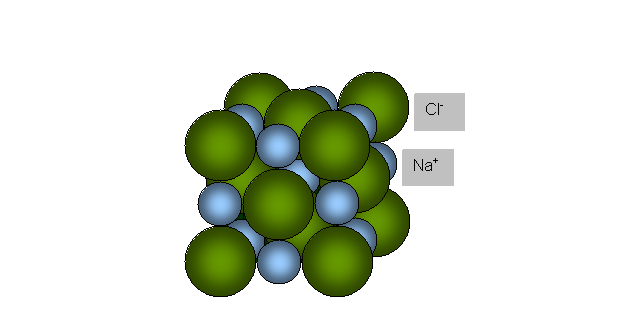
Рис.19
Структурные же схемы металлических кристаллов,
образованных атомами одного химического элемента, даются в виде одинаковых
шаров. За основу здесь, вероятно, берется принцип однородности частиц в
кристалле. К сожалению даже рентгеноструктурный анализ не дает никаких сведений
о размерах атомов. Он позволяет определять, хотя и очень точно, только
расстояния между центрами смежных частиц в веществе. Поэтому радиусы однородных
атомов в кристаллах берутся как r = d / 2, где константа d – ближайшее
расстояние между центрами двух соседних частиц в элементарной ячейке кристалла
(рис.20).
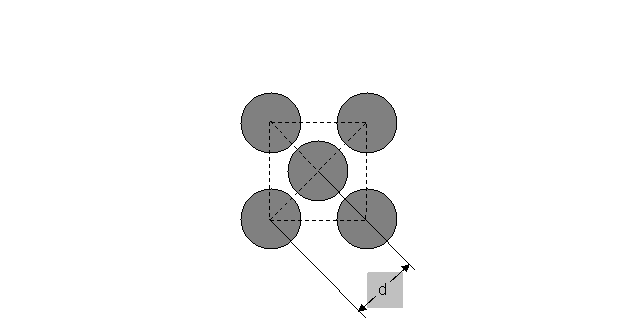
Рис.20 Схема расположения атомов в узлах одной грани
элементарной ячейки кристалла алюминия (Al)
Но, во-первых, как уже говорилось выше, необходимым условием образования устойчивой взаимосвязи между двумя ближайшими атомами в кристалле является их объединение с противоположно направленными магнитными моментами. А два замкнутых электрических контура с токами противоположного направления, находящиеся во внешнем магнитном поле, должны подвергаться деформации: один контур – сжатию, другой – растяжению. Аналогичная реакция на действие стороннего магнитного поля с соответствующими параметрами, очевидно, присуща и контурам атомного масштаба. И если такое представление о деформации оболочек атомов верно, то любая модель кристалла должна содержать признак обозначенного магнитного эффекта в виде шаров разного диаметра даже для структур, образованных из однородных частиц.
Во-вторых. Принято считать, что каждый атом в узле кристаллической решетки колеблется подобно маятнику независимо от своих соседей и, например, при нагреве интенсивность теплового движения увеличивается вплоть до того, что атомы покидают свое место «в строю», разрушая при этом кристалл.
Но представим себе несколько другую картинку. Предположим, что при термическом нагревании кристалла алюминия причиной изменения параметров его кристаллической решетки (например, объемного расширения) является увеличение размеров атомов с одинаково направленными векторами магнитных моментов. А процесс плавления металла начинается, образно говоря, с «короткого замыкания» встречных токов этих атомных микроконтуров, сблизившихся до критического предела (рис.21). При нормальных же температурных условиях (0°С) существования кристалла его атомы в узлах пространственной решетки, вероятно, «чувствуют себя гораздо комфортнее».
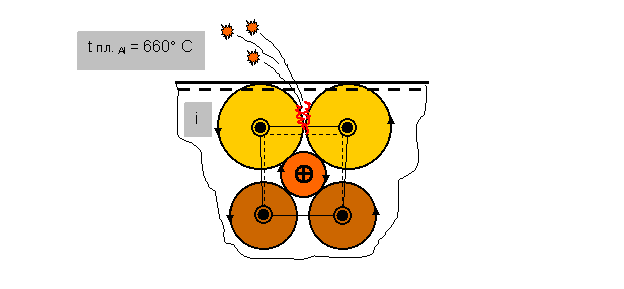
Рис.21 Схема «короткого замыкания» встречных токов (i ) атомных микроконтуров в кристалле алюминия
Рассуждать здесь будем следующим образом. Если дается большое количество маленьких шариков равного диаметра и какой-нибудь ящик, то для того, чтобы поместить в него максимальное число этих шариков, их нужно укладывать в определенном порядке. Как известно, одной из наиболее плотных упаковок является кубическая гранецентрированная (рис.22). Она обеспечивает укладку шариков с коэффициентом k = 0,74.
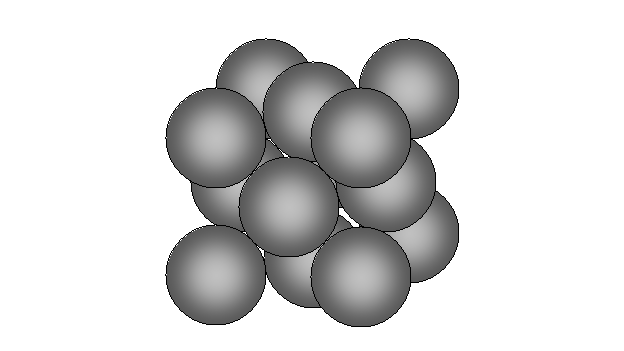
Рис.22
То есть, суммарный объем (S Vо) одинаковых шариков, уложенных в кубический ящик единичного объема указанным способом, составит 0,74 м3. Это больше коэффициента случайного заполнения примерно на 20 %.
Теперь вычислим объем (Vо) одного из таких шариков, как если бы он имел средний размер атома алюминия и в числе других заполнял условный «кристаллический ящик» кубической формы и единичного объема при указанной упаковке:
![]() м3, (58)
м3, (58)
где: k = 0,74 – коэффициент заполнения ящика шариками;
М = 26,98 – относительная атомная масса алюминия;
NA = 6,02*1026 кмоль-1 – число Авогадро;
r = 2,7*103 кг / м3 – плотность алюминия в данном примере.
Отсюда, константа d пространственной решетки кристалла алюминия при нормальной температуре (0°С) примерно равна:
![]() м.
(59)
м.
(59)
Рассмотрим схему (рис.23) одной грани элементарной ячейки кристалла алюминия. Определим радиусы R и r ее углового и центрального атомов при нормальных температурных условиях. Будем полагать, что максимально-допустимый радиус R max углового атома грани при указанных условиях является предельным, так как его дальнейшее увеличение (например, при нагревании кристалла) приведет к изменению параметров пространственной решетки, в частности – константы d.
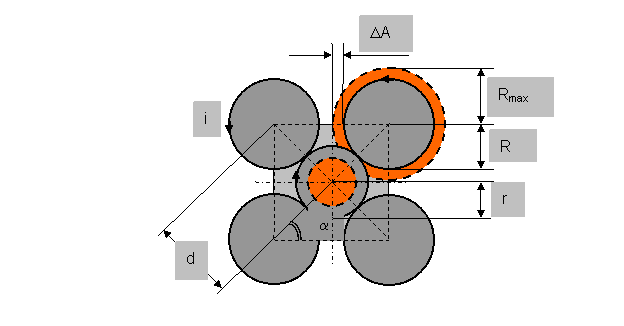
Рис.23 Схема одной грани элементарной ячейки кристалла алюминия
d – константа пространственной решетки (ближайшее расстояние между центрами двух соседних атомов в ячейке);
R max – максимально-допустимый радиус угловых атомов ячейки при 0°С;
R и r – средние радиусы центрального и угловых атомов ячейки в данных условиях;
a = 45°;
DА – амплитуда изменения радиуса атома от его среднего значения при 0°С (в модельном представлении,
где атомы колеблются подобно маятникам относительно узлов пространственной решетки, DА является
амплитудой этих колебаний и зависит от температуры.
Итак, максимально-допустимый радиус (R max) углового атома грани при указанных условиях примерно равен:
R max = d cos a = 2,8*10-10 cos 45 ° = 2*10-10 м. (60)
Амплитуда (DА) изменения радиуса атома от его среднего значения при 0°С в кристалле алюминия может быть в пределах:
![]() м,
(61)
м,
(61)
где: k = 1,38*10-23 Дж
/ К – постоянная Больцмана;
Т = 273,15 К – значение температуры по термодинамической шкале;
Е = 7,1*1010 Н / м2 – модуль упругости алюминия;
d = 2,8*10-10 м – константа кристаллической решетки алюминия.
В таком случае среднее значение радиуса (R) углового атома ячейки при нормальной температуре получается равным:
R = R max – DA = 2*10-10 – 1,9*10-11 = 1,8*10-10 м, (62)
а средний радиус (r) центрального атома грани в этих условиях будет иметь величину:
r = d – R = 2,8*10-10 – 1,8*10-10 = 1*10-10 м. (63)
Теперь ознакомимся с магнитными свойствами атома алюминия, имеющего в нормальном состоянии основной терм – 2 Р 1 / 2. Для этого терма (при J = 1 / 2, S = 1 / 2, L = 1) множитель Ланде равен g = 2 / 3 = 0,67. Отсюда, усредненный по времени магнитный момент атома алюминия (P/M Al ), создаваемый одним его некомпенсированным электроном 3р1, примерно равен:
![]() А * м2. (64)
А * м2. (64)
Поскольку атом алюминия располагает тремя валентными электронами, то его магнитный момент в кристалле, очевидно, возрастает в 3 раза и достигает величины (P//M Al):
Р//М Al = Р/М Al * 3 = 5,4*10-24 * 3 = 1,6*10-23 А * м2. (65)
Тогда сила тока i R условного плоского электрического контура, образованного тремя валентными электронами атома алюминия при его среднем радиусе R и площади этого контура S R = p R2, может быть равной:
![]() А.
(66)
А.
(66)
Соответственно, ток i r контура с радиусом r и площадью S r = p r 2 будет иметь величину:
![]() А.
(67)
А.
(67)
Разница между значениями этих двух токов противоположного направления (Di) на поверхности алюминиевого кристалла составляет:
Di = i r – i R = 5,1*10-4 – 1,6*10-4 = 3,5*10-4 А. (68)
Дальше уже знакомо: если элементарный ток Di определенного направления существует на межатомном расстоянии d, то суммарная величина таких токов (S Di) на отрезке в 1 м получается равной:
![]() А.
(69)
А.
(69)
Отсюда, магнитный момент РМ 1 условного замкнутого электрического контура в виде квадратной рамки единичной площади (1 м2) и током в нем I = S Di приблизительно равен:
РМ 1 = I S = 6*105 * 1 = 6*105 А * м2. (70)
Если представить себе кристалл алюминия кубической формы и единичного объема, условно состоящего из набора таких рамок-контуров, то их количество (n) в данной модели соответствовало бы числу атомов алюминия, уместившихся на линии ребра этого кристалла:
![]() шт.
(71)
шт.
(71)
Тогда общий магнитный момент РМ этой «конструкции» должен быть близким по величине магнитному моменту реального кубометра алюминия:
РМ = РМ 1 * n = 6,0*105 * 4,4*109 = 2,6*1015 А * м2. (72)
Все вышеизложенные рассуждения в данном примере относительно РМ можно выразить следующей формулой и ее числовым значением (см. рис.23):
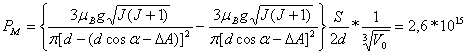 А * м2, (73)
А * м2, (73)
где: m В = 9,3*10-24 А * м2 – магнетон Бора;
g = 0,7 – множитель Ланде для основного терма атома алюминия (2 Р 1 / 2);
J = 1 / 2 = 0,5 – квантовое число полного момента количества движения атома алюминия;
S = 1 м2 – площадь сечения куба (параллельно одной из его граней);
a = 45°;
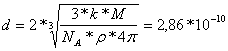 м – константа кристаллической решетки
алюминия; (74)
м – константа кристаллической решетки
алюминия; (74)
![]() м3 – средний объем атома
алюминия; (75)
м3 – средний объем атома
алюминия; (75)
где: k = 0,74 – коэффициент суммарного объема атомов алюминия в условном кристалле кубической формы и единичного объема;
М = 26,98 – относительная атомная масса алюминия;
NA = 6,02*1026 кмоль-1 – число Авогадро;
r = 2,7*103 кг / м3 – плотность алюминия в данном примере.
![]() м – амплитуда колебаний атомов в кристалле
алюминия при 0°С.
Или амплитуда изменения радиуса
м – амплитуда колебаний атомов в кристалле
алюминия при 0°С.
Или амплитуда изменения радиуса
электронных оболочек атомов (предположение автора – И. В.); (76)
где: k =
1,38*10-23 Дж / К – постоянная Больцмана;
Т = 273,15 К (кельвин) –
значение температуры по термодинамической шкале;
Е = 7,1*1010 Н / м2 – модуль упругости алюминия.
В итоге сила FM электромагнитного притяжения «куска» алюминия кубической формы и единичного объема, покоящегося на поверхности Земли в районе ее геомагнитного экватора, получается равной:
![]() Н. (77)
Н. (77)
Итак, результаты вычислений в примерах с объектами, покоящимися на поверхности Земли, можно считать вполне весомым аргументом в пользу рассматриваемой гипотезы. Но поскольку гравитация имеет статус всемирного физического явления, доказательную часть обсуждаемого вопроса придется несколько расширить.
Примечание
7: величину
электрического заряда (q)
исследуемого объекта или его магнитного момента (РМ ) можно быстро
определить через его массу m, используя
следующие коэффициенты(k q и k M
):
![]() k q = 8*10 -2
Кл / кг – для вычисления заряда q объекта через его массу m
(например: q NaCl = k q
* m NaCl );
k q = 8*10 -2
Кл / кг – для вычисления заряда q объекта через его массу m
(например: q NaCl = k q
* m NaCl );
![]() k M
=1*1012
А * м2 / кг – для
вычисления магнитного момента P М объекта через его массу m (например: Р
М NaCl = k M * m NaCl ) .
k M
=1*1012
А * м2 / кг – для
вычисления магнитного момента P М объекта через его массу m (например: Р
М NaCl = k M * m NaCl ) .
Примечание 8: изложенные выше
рассуждения и примеры, подкрепленные расчетами, позволяют также уяснить
сущность такого свойства физического тела, как его масса (инертность). Можно
полагать, что инертные качества физического объекта, находящегося в
электромагнитном поле, характеризуются результирующим магнитным моментом его
поверхностных атомов.
___________________________________________________________________________________________________