Гравитация «электромагнитная»

                                             

 

Рассмотрим с позиций  «гравитации», «электростатики» и «магнетизма» в пределах интересующей нас задачи несколько примеров с физическими объектами, покоящимися на земной поверхности. Здесь нужно заметить, что на каждый подобный объект должны воздействовать многие природные силы и факторы. Но, сокращая предмет обсуждения и пренебрегая, например, такой их составляющей как центростремительная сила (связанная с суточным вращением Земли), оставим для рассмотрения только силу, которая называется весом или, по нашему предположению, силой электромагнитного притяжения объекта к земной поверхности.

 

Притяжение к поверхности Земли монолитного объекта из каменной соли

 

Используя умозрительный прием, представим себе в качестве первого объекта кристалл каменной соли (хлорида натрия – NaCl) в виде монолитного куба единичного объема (1 м³). Для того чтобы упростить последующие расчеты, «поместим» наш объект на земной поверхности в точке пересечения географического и геомагнитного экваторов планеты.

 

Приравняем гравитационную силу F_G, с которой данный объект должен притягиваться к Земле, к его весу Р. Для покоящегося на земной поверхности тела: 

P » m G,     (1)

 

где:

Р – вес тела, Н (ньютон);  m – масса тела, кг (килограмм); G – напряженность гравитационного поля Земли, численно равная величине ускорения свободного падения (ср. значение в районе экватора на уровне моря примерно равно 9,78 м / с²), Н / кг.                               

                            

Плотность хлорида натрия r = 2173 кг / м³  [1]. Другими словами, масса m кристалла NaCl при его объеме в 1 м³ должна быть равной 2173 кг. Отсюда, вес Р данного тела примерно равен: 

 

Р » m G = 2,17*10³ * 9,78 = 2,12*10⁴ Н.     (2)

 

Теперь, полагаясь на принятую к рассмотрению гипотезу, с учетом «демонстративного» совпадения по форме законов тяготения и электростатики, осмелимся считать вес (Р) физического объекта, покоящегося на поверхности Земли, эквивалентом силы (F_E ) его электростатического притяжения к земной поверхности.

 

Естественно, подобное допущение предполагает наличие соответствующего заряда  у этого объекта и электрического поля у поверхности Земли (или наоборот), достаточных для такого их взаимодействия по закону Кулона:

 

F_E = q E,     (3)

 

где:  F_E – сила электростатического взаимодействия рассматриваемого объекта с Землей у ее поверхности, Н;  

        q – электрический заряд объекта, Кл (кулон);

        Е – напряженность электрического поля Земли, В / м (вольт / метр). 

 

Исследования показали, что у земной поверхности существует стационарное электрическое поле с напряженностью Е, в среднем равной около 130 В / м. Наибольшие значения Е имеет в средних широтах, а к полюсам и экватору убывает.

 

 

Считая земной шар на фоне космических просторов всего лишь точечным зарядом, можно полагать, что вектор Е напряженности стационарного электрического поля Земли направлен от ее, скажем, уровенной поверхности вверх и ей в основном перпендикулярен. Косвенным аргументом в пользу такого предположения может служить порядок распределения заряженных частиц в ионосфере Земли [2]. Самые внешние слои ионосферы состоят практически из одних протонов (Н⁺). В нижней ионосфере преобладают отрицательные ионы и просто электроны (е ^-). Если к такому распределению заряженных частиц по высоте причастно и электрическое поле Земли, то вектор Е этого поля, естественно, должен быть направлен от ее поверхности вверх.

 

По аналогии с расчетом Е для равномерно заряженного шара за пределами его объема будем полагать, что напряженность электрического поля у поверхности Земли (E_Z) в этом месте примерно равна:

 

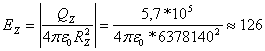  В / м,     (4) 

 

где:  Q_Z » 5,7*10⁵ Кл – величина электрического заряда на поверхности Земли [1];

        R_Z = 6378140 м – экваториальный радиус нашей планеты [3];

        4pe₀ = 1,11265*10^-10 Кл² / Н * м²  (где: e₀ – электрическая постоянная).

 

Тогда в общих чертах сущность земного тяготения сквозь призму электростатики может выглядеть следующим образом. Электрическое поле Земли воздействует на электронные оболочки атомов, образующих поверхность монолитного тела, с силой F_i на каждую из них. Эта сила должна сообщать импульс поступательного движения оболочке, а значит и всему атому в целом, заставляя его смещаться против направления вектора напряженности Е электрического поля Земли. Стремление атомов поверхностного слоя сместиться под воздействием внешнего электрического поля в свою очередь передается через межатомные связи и всем остальным частицам в объеме этого тела. Силы F_i (составляющие) можно свести к одной равнодействующей силе F_E , олицетворяющей силу электростатического притяжения тела к Земле (или его вес Р):

 

S F_i = F_E = P     (5)

 

Почему электронные оболочки только поверхностных атомов? Не углубляясь в этот вопрос, можно полагать, что внутри объема монолитного вещества суммарный электрический заряд ядер атомов и их оболочек равен нулю. А заряд электронных оболочек атомов на поверхности тела остается некомпенсированным. В результате электрическое поле Земли может воздействовать на любой физический объект непосредственно и в первую очередь только через отрицательно заряженные оболочки его поверхностных атомов. Так что, в соответствии с рекомендациями древних мудрецов будем искать «истину на поверхности».

 

Обратимся теперь к внутренней структуре кристалла NaCl [4]. Необходимо будет определить суммарную величину заряда электронных оболочек поверхностных атомов рассматриваемого объекта.                                                                                                                      

 

В кристалле каменной соли атомы натрия (Na) и хлора (Cl) образуют пространственную решетку в виде правильной трехмерной кубической сетки. Подробнее об электронных конфигурациях и взаимодействии ионов в кристалле изложено в статье «Как устроен механизм гравитации» (часть1, пример1) на http://man3.narod.ru/gravitatsiya/index.html .

 

Суммарный заряд (q) электронных оболочек атомов натрия и хлора, образующих поверхностный слой кристалла каменной соли кубической формы и единичного объема, примерно равен:

 

 Кл,     (6)

 

где:  e = – 1,6*10^-19 Кл – заряд электрона;

        n _Na = 11 – количество электронов в оболочке отдельно взятого атома натрия;

        n _Cl = 17 – количество электронов в оболочке отдельно взятого атома хлора;

        d = 2,79*10^-10 м – константа (ближайшее расстояние между центрами двух соседних частиц в элементарной ячейке кристалла NaCl).

 

Примечание 1:  этого заряда (q) «опасаться» не следует. Он всего лишь соответствует суммарному значению атомных токов натрия и хлора на поверхности кристалла NaCl площадью в 6 м² за период времени порядка 10^–14 с и является просто условно-расчетной величиной. Реальная же сила этих токов в кристалле примерно равна 10^–4 ампер, а человек начинает ощущать ток с величины 10^–3 А (пороговая реакция). Так что, употребляя поваренную соль, можно смело сочетать приятное (вкусовое раздражение) с полезным (подзарядкой  своих  телесных  клеток  током  супервысокой  частоты). В меру, конечно.

 

В итоге электростатическая сила (F_E ) притяжения к Земле монолитного кубометра каменной соли получается равной:

 

F_E = q E = – 1,7*10²  * 1,26*10²  = – 2,1*10⁴ Н.     (7)

 

Как видим, полученные значения сил P и F_E находятся друг с другом в согласии. Знак «минус» у результата вычисленной силы F_E указывает на то, что она является силой притяжения, а не отталкивания.

 

Примечание 2: силу (F_E ) электростатического притяжения к поверхности Земли объекта с любыми формами и размерами можно вычислить по формуле:

 

F_E = F₁ (V / V₁),     (8)

 

где:  F₁ = q E – сила притяжения к Земле монолитного вещества, из которого состоит данный объект,

                         кубической формы и единичного объема, Н; 

        V₁ = 1 м³ – единичный объем;

        V  – объем рассматриваемого монолитного объекта

                (или суммарный объем монолитных деталей, из которых этот объект состоит), м³.

 

Примечание 3:  электрический заряд (q ) объекта можно выразить через его массу (m ) и коэффициент k _e:    

 

q = k _e *  m,     (9) 

 

где:   k _e » 8*10^-2 Кл / кг – коэффициент (k _e = G / E, где G – напряженность гравитационного поля Земли;

                                                                     Е – напряженность электрического поля Земли в данном месте).

         m – масса объекта, кг.

 

Таким образом, уже появляется некоторое основание считать, что рациональное зерно в предложенной гипотезе присутствует. Но полученный результат, естественно, требует подтверждения своей закономерности. И вполне очевидно, что если данная гипотеза действительно отражает объективную реальность, то и в рамках понятий о магнетизме мы должны получить в этом примере такой же или близкий к нему результат. 

 

 

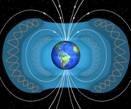
Рассматривая оборотную сторону «гравитационной медали», попробуем увязать гравитацию с электромагнетизмом на следующей основе. Представим, что Земля и данный объект притягиваются друг к другу как два магнита в соответствии со своими размерами.

 

В первом приближении магнитное поле Земли подобно полю гигантского магнитного диполя, расположенного в центральных частях земного шара, с Южным магнитным полюсом в северном полушарии и с Северным магнитным полюсом в южном полушарии Земли. Магнитный момент (Р_{М Z} ) этого диполя примерно равен 8*10¹⁵ А * м² (ампер * метр кв.) [5].  

 

Положим в основу наших дальнейших рассуждений об электромагнитной природе земного притяжения формулу:

 

 ,     (10)

 

где:  F_M – сила электромагнитного притяжения физического тела к Земле, Н;

        Р_М – магнитный момент этого тела, А * м²;

        DB_Z / Dh – средняя скорость изменения индукции магнитного поля (B_Z) Земли

                          по высоте (h) в слое до 1 м от ее уровенной поверхности, Тл / м (тесла / метр). 

 

Определим среднюю скорость изменения индукции магнитного поля Земли (DВ_Z / Dh) в месте пересечения ее магнитного экватора с экватором географическим. Будем считать, что в таком месте силовые линии магнитного поля в метровом слое от земной поверхности должны быть ей параллельны. Итак:

 

 ,     (11)

где:

 

  Тл,     (12) – величина индукции магнитного поля Земли у ее поверхности

                                                                                     на геомагнитном экваторе в точке пересечения его с экватором географическим [2];

 

                                                где:  P_{M Z}  = 8*10¹⁵ А * м² – магнитный момент земного диполя;

                                                        R_Z = 6378140 м – расстояние от центра Земли до ее поверхности в районе географического экватора;

                                                       Ф = 0° – геомагнитная широта (градус).

 

  Тл.     (13) – величина индукции магнитного поля Земли

                                                                                                                                                   на высоте h = 1 м от земной поверхности.

 

Примечание 4: ввиду того, что величины В¢_Z  и В²_Z  в слое Dh = 1 м мало отличаются друг от друга, результаты вычислений в формулах (12) и (13) представлены семью значащими цифрами.

 

В итоге средняя скорость изменения индукции магнитного поля Земли (DВ_Z / Dh) в районе геомагнитного экватора в метровом слое от ее поверхности получается равной: 

 

  Тл / м.     (14)

 

Полагая, что магнитное поле Земли воздействует на атомы поверхностного слоя вещества как на микроконтуры с током, определим результирующий магнитный момент поверхностных атомов нашего объекта.

 

Опуская промежуточные рассуждения, магнитный момент (Р_М) условного кристалла каменной соли кубической формы и единичного объема выразим следующей формулой и ее числовым значением:

 

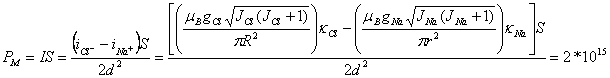  А * м²,     (15)

 

где: I – общая результирующая сила тока электронных оболочек поверхностных ионов Cl^- и Na⁺ рассматриваемого объекта;     

      S – площадь сечения куба каменной соли (параллельно одной из его граней и перпендикулярно силовым линиям магнитного поля В);

        i _Cl^-   – сила тока в электронной оболочке иона хлора (Cl^-);

        i _Na⁺ - сила тока в оболочке иона натрия (Na⁺);

       d = 2,79*10^-10 м – константа кристаллической решетки каменной соли;

       m _В = 9,3*10^-24 А * м² – магнетон Бора;

        g _Cl = 1,3 – множитель (фактор) Ланде для основного терма атома хлора (² Р_{3 / 2});

        g _Na = 2 – множитель Ланде для основного терма атома натрия (² S_{1 / 2});

        J _Cl = 3 / 2 – квантовое число полного момента количества движения  атома хлора;

        J _Na = 1 / 2 – квантовое число полного момента количества движения атома натрия;

        R = 1,81*10^-10 м – эффективный радиус иона хлора (Cl^-) в кристалле NaCl;

        r = 9,8*10^-11 м – эффективный радиус иона натрия (Na⁺) в этом кристалле;

        k _Cl  = 1,8;  k _Na  = 0,2.

 

Примечание 5:  в отношении коэффициентов k _Cl  и  k _Na  можно пояснить следующее. При взаимодействии двух атомов (Na и Cl) с образованием из них связанной пары ионов (Na⁺ и Сl^-) атом хлора как бы «оттягивает» на себя согласно экспериментальным данным около 80 %  облака валентного электрона атома натрия (с орбитали 3s¹). В результате этого валентный электрон атома натрия лишается 0,8 элементарного электрического заряда. Поэтому в формуле (15) поправочный коэффициент k _Na = (1 – 0,8) = 0,2. Соответственно, валентный электрон  атома хлора  приобретает  0,8 элементарного электрического заряда. Отсюда, коэффициент  k _Cl = (1 + 0,8) = 1,8.

 

О содержании формулы (15) более подробно говорится в развернутой статье «Как устроен механизм гравитации» на web-странице  http://man3.narod.ru/gravitatsiya/chast_2.htm  (2.1. Магнитные свойства вещества).   

 

В результате расчетная величина электромагнитной силы (F_M) притяжения кубического кристалла каменной соли единичного объема примерно равна:

 Н.     (16)

 

В данном примере пришлось сопрягать между собой физические параметры широкого диапазона (от микро- до макровеличин) в приблизительных их значениях. Но, думается, что разницу между полученными значениями веса Р = 2,12*10⁴ Н и сил: F_E = – 2,1*10⁴ Н,  F_M = 2*10⁴ Н можно считать вполне приемлемой. 

 

Теперь, чтобы убедиться в добротности обсуждаемой гипотезы, перейдем от примера с камнем к рассмотрению металла. К числу металлов относится около 75 % всех известных в настоящее время элементов.

 

Притяжение к земной поверхности объекта из алюминия

 

Кристалл алюминия (Al) имеет кубическую плотнейшую гранецентрированную решетку. Если плотность его r = 2710 кг / м³, то вес (Р) этого металла кубической формы и единичного объема на уровне моря в районе экватора должен быть равным:

 

P » m G = 2,71*10³ * 9,78 = 2,65*10⁴ Н.     (17)

 

Отдельно взятый атом алюминия содержит в своей оболочке три валентных электрона. При зарождении кристалла два таких возбужденных атома, очевидно, могут объединить распаренные электроны в дублеты, достраивая свои подуровни тремя привлеченными электронами из оболочки атома-партнера. В этом случае взаимодействующий атом, оттягивая на себя электроны из оболочки партнера, скорее всего, может «рассчитывать» только на половину их электрического заряда, так как  здесь в образовании связанной пары участвуют уже равноправные партнеры (атомы одного сорта). Таким образом, будем полагать, что каждый поверхностный атом кристалла алюминия получает в процессе взаимодействия от трех привлеченных электронов партнера дополнительный заряд, как бы эквивалентный заряду полутора электронов.

 

Тогда общий электрический заряд (q) электронных оболочек поверхностных атомов условного монолитного кристалла Al кубической формы и единичного объема должен приблизительно составить:

 

q = [e (n + 1,5) N] k = – 2,1*10² Кл,     (18)

 

где:  е = – 1,6*10^-19 Кл – заряд электрона;

        n = 13 – количество электронов в оболочке отдельно взятого атома алюминия;

        k = 6 – количество граней куба;

 

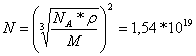         (19) – количество атомов алюминия в поверхностном слое его кристалла на площади 1 м²,

                                                                    где:  N_A = 6,022*10²⁶ кмоль^-1 – число Авогадро;

                                                                            r = 2710 кг / м³ – плотность алюминия в данном примере;

                                                                            М = 26,98 – относительная атомная масса алюминия;

                                                

В таком случае сила (F_E) электростатического притяжения алюминиевого монокристалла кубической формы и единичного объема к Земле на уровне моря в районе экватора получается равной:

 

F_E = q E = – 2,1*10² * 1,26*10² = – 2,65*10⁴ Н.     (20)

 

Результаты этого примера (P = 2,65*10⁴ Н и F_E = – 2,65*10⁴ Н), рассмотренного с позиций «гравитации» и «электростатики», также обнадеживают. Посмотрим теперь на это дело с «электромагнитной колокольни».

 

 

Общий магнитный момент (Р_М) данного алюминиевого объекта при температуре 0°С приблизительно равен:

 

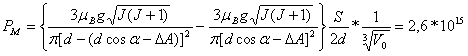 А * м²,     (21)

 

где:  m _В = 9,3*10^-24 А * м² – магнетон Бора;

        g = 0,7 – множитель Ланде для основного терма атома алюминия (² Р _{1 / 2});

        J = 1 / 2 – квантовое число полного момента количества движения атома алюминия;

        S = 1 м² – площадь сечения куба (параллельно одной из его граней);

        a = 45°;

 

         м³     (22) – средний объем атома алюминия;

 

                                                                       где: k = 0,74 – коэффициент суммарного объема атомов алюминия в условном кристалле

                                                                                               кубической формы и единичного объема;                           

                                                                               М = 26,98 – относительная атомная масса алюминия;

                                                                               N_A = 6,02*10²⁶ кмоль^-1 – число Авогадро;

                                                                               r = 2,7*10³ кг / м³ – плотность алюминия в данном примере; 

         м     (23) – амплитуда изменения радиуса атома от его среднего значения при 0°С

                                                             (подробнее см. http://man3.narod.ru/gravitatsiya/index.html , 2.2 «Динамическая модель гравитации»),

 

                                                                                             где:   k = 1,38*10^-23 Дж / К – постоянная Больцмана; 

                                                                              Т = 273,15 К – значение температуры по термодинамической шкале;

                                                                              Е = 7,1*10¹⁰ Н / м² – модуль упругости алюминия;

                                                                              d = 2,8*10^-10 м – константа кристаллической решетки алюминия.

 

                                                                    (в модельном представлении, где атомы колеблются подобно маятникам относительно узлов

                                                                     пространственной решетки, DА является амплитудой этих колебаний и зависит от температуры).

 

В итоге сила F_M электромагнитного притяжения «куска» алюминия кубической формы и единичного объема, покоящегося на поверхности Земли в районе ее геомагнитного экватора, получается равной:

 

 Н.     (24)

 

Примечание 6:  величину магнитного момента (Р_М ) исследуемых объектов в данном месте ориентировочно можно определить через их массу m, используя коэффициент k _M  » 9,8*10¹¹  А * м² / кг (где: k _M = G / (DB / Dh)):

 

Р_М  = k _M *  m     (25)     

 

Примечание 7:  изложенные выше рассуждения и примеры, подкрепленные расчетами, позволяют также уяснить сущность такого свойства физического тела, как его масса (инертность). Можно полагать, что инертные качества физического объекта, находящегося в электромагнитном поле, характеризуются результирующим магнитным моментом его поверхностных атомов и от него зависят.

 

Примечание 8:  следует сказать, что в предлагаемую схему объяснения природы гравитации укладываются не только рассмотренные здесь кристаллы с ионной и металлической пространственными решетками, но и другие вещества, в том числе с молекулярной структурой их внутреннего строения (например, вода – Н₂О; см. http://man3.narod.ru/gravitatsiya/index.html ; ч.1, Пример 3).

 

Итак, результаты вычислений в примерах с объектами, покоящимися на поверхности Земли, можно считать вполне весомым аргументом в пользу рассматриваемой гипотезы. Но поскольку гравитация имеет статус всемирного физического явления, доказательную часть обсуждаемого вопроса придется несколько расширить.