ГРАВИТАЦИЯ «ЭЛЕКТРОСТАТИЧЕСКАЯ»

1. 1. Истина познается в сравнении

 

 

Посмотрим на изящные формулы законов Ньютона (1) и французского физика Кулона (2), описывающие гравитационное и электростатическое взаимодействия между двумя физическими объектами. Сравним их по содержанию:

 

 

Шарль Кулон (1736 – 1806)

 

F_G = g (m M / R²)     (1)

 

F_G – сила гравитационного взаимодействия между двумя физическими телами, Н (ньютон);

m, M – массы взаимодействующих тел, кг (килограмм);

R – расстояние между центрами масс данных тел, м (метр);

g – гравитационная постоянная, Н * м² / кг²;

 

g (M / R²) – выражение, выделенное из формулы (1), имеет смысл напряженности гравитационного поля (G) тела с массой М, Н / кг.

                   Напряженность гравитационного поля – величина векторная. Направление вектора G совпадает с направлением силы F_G

                   (рис.1).

 

Рис.1

 

F_E = k (q Q / R²)     (2)

 

F_E – сила электростатического взаимодействия между двумя заряженными телами шарообразной формы, Н (ньютон);

q, Q – поверхностные (объемные) заряды взаимодействующих тел, Кл (кулон);

R – расстояние между центрами заряженных шаров, м (метр);

k ­– коэффициент пропорциональности, Н * м² / Кл²;

 

k (Q / R²) – выражение, выделенное из формулы (2), имеет смысл напряженности электрического поля (Е) тела с зарядом Q,

                   В / м (вольт / метр).

                   Напряженность электрического поля – величина векторная. Направление вектора Е совпадает с направлением силы F_E ,

                   действующей на положительный заряд (q⁺), и противоположно ему, если заряд отрицательный (q^-)

                   (рис.2).

 

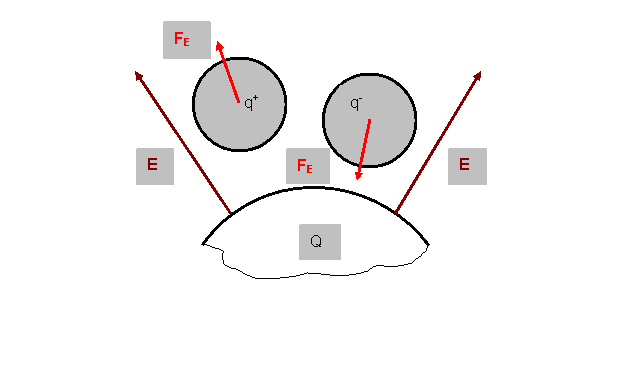
Рис.2

 

Формулы (1) и (2) можно упростить:

                                                               если g (M / R²) = G, то F_G = m G     (3),

                                                               если k (Q / R²) = E, то  F_E = q E      (4).

 

Как видим, форма и содержание данных формул вызывают ощущение их определенной родственной гармонии. Конечно, в силу исторических причин у этих формул-сестер разные отцы-ученые, но мать-Природа у них явно одна. Скорее всего, и говорят эти невольно разлученные «сестры» об одном и том же, только на разных языках, поскольку механика была основана на одном «комплекте» способов измерения физических величин, электростатика же - на другом, существенно отличном от первого.

 

Тогда, полагаясь на принятую к рассмотрению гипотезу с учетом «демонстративного» совпадения по форме законов тяготения и электростатики, осмелимся считать вес физического объекта, покоящегося на поверхности Земли, эквивалентом силы его электростатического притяжения к земной поверхности.

 

Естественно, подобное допущение предполагает наличие соответствующего заряда у этого объекта и электрического поля у поверхности Земли (или наоборот), достаточных для такого их взаимодействия.

 

Исследуем «гравитационную медаль» с ее электростатической стороны. В специальном разделе теории электричества и магнетизма, который называется электростатикой, рассматриваются свойства тел и частиц, обладающих электрическим зарядом и неподвижных в инерциальной системе отсчета, а также их взаимодействие между собой. Инерциальной называется система отсчета, в которой свободная  материальная точка (тело) покоится или движется прямолинейно и равномерно. Покой точки (тела) является частным случаем  инерциального движения. Нередко инерциальную систему отсчета связывают с Землей, пренебрегая при этом  вращением планеты вокруг собственной оси и ее движением вокруг Солнца.

_______________________

      

 

 

1. 2. Статический макет механизма гравитации

 

Как известно, на поверхности нашей планеты имеется некоторый избыточный электрический заряд. Исследования показали, что у земной поверхности существует стационарное электрическое поле с напряженностью Е, в среднем равной около 130 вольт / метр. Наибольшие значения Е имеет в средних широтах, а к полюсам и экватору убывает. [1]. 

 

 

Считая земной шар на фоне космических просторов всего лишь точечным зарядом, можно полагать, что вектор Е напряженности стационарного электрического поля Земли направлен от ее, скажем, уровенной поверхности вверх и ей в основном перпендикулярен. Косвенным аргументом в пользу такого предположения может служить порядок распределения заряженных частиц в ионосфере Земли [2]. Самые внешние слои ионосферы состоят практически из одних протонов (Н⁺). В нижней ионосфере преобладают отрицательные ионы и просто электроны (е^-). Если к такому распределению заряженных частиц по высоте причастно и электрическое поле Земли, то вектор Е этого поля, естественно, должен быть направлен от ее поверхности вверх (рис.3).

 

 

Рис.3

 

Данное направление вектора Е напряженности электрического поля Земли допускает возможность электростатического притяжения физического объекта к земной поверхности только при условии, если он имеет какой-то электрический заряд отрицательного знака (q^–). В таком случае возникает закономерный вопрос: что может являться источником подобного заряда у обыкновенного физического тела?

 

Если рассуждать просто, то любой физический объект состоит из атомов. Считается, что ядра атомов заряжены положительно, а их электронные оболочки являются носителями заряда отрицательного. И похоже на то, что именно электронные оболочки атомов, выходящих на поверхность монолитного тела, как раз и могут иметь самое прямое отношение к искомому заряду q^– .

 

Почему электронные оболочки только поверхностных атомов? Не углубляясь в этот вопрос, можно полагать, что внутри объема монолитного вещества суммарный электрический заряд ядер атомов и их оболочек равен нулю. А заряд электронных оболочек атомов на поверхности тела остается некомпенсированным. В результате электрическое поле Земли может воздействовать на любой физический объект непосредственно только через отрицательно заряженные оболочки его поверхностных атомов. Так что, в соответствии с рекомендациями древних мудрецов будем искать «истину на поверхности». 

 

Итак, в общих чертах сущность земного тяготения сквозь призму электростатики выглядит следующим образом. Электрическое поле Земли воздействует на электронные оболочки атомов, образующих поверхность монолитного тела, с силой F_i на каждую из них. Эта сила должна сообщать импульс поступательного движения оболочке, а значит и всему атому в целом, заставляя его смещаться против направления вектора Е электрического поля Земли. Стремление атомов поверхностного слоя сместиться под воздействием внешнего электрического поля в свою очередь передается через межатомные связи и всем остальным частицам в объеме этого тела (рис.4).

 

 

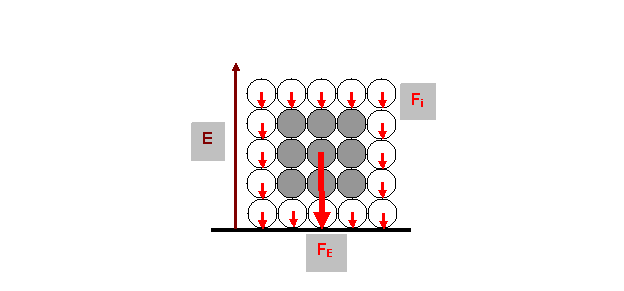
Рис.4

 

Cилы F_i (составляющие) можно свести к одной равнодействующей силе F_E , олицетворяющей силу электростатического притяжения тела к Земле (или его вес Р):

S F_i = F_E = P     (5)

 

А теперь рассмотрим с позиций гравитации и электростатики в пределах интересующей нас задачи несколько примеров с физическими объектами, покоящимися на земной поверхности. Здесь нужно заметить, что на каждый подобный объект должны воздействовать многие природные силы и факторы. Но, сокращая предмет обсуждения и пренебрегая, например, такой их составляющей как центростремительная сила (связанная с суточным вращением Земли), оставим для рассмотрения только силу, которая называется весом или, по нашему предположению, силой электростатического притяжения объекта к земной поверхности.

 

Для того чтобы упростить последующие расчеты, «поместим» наши объекты на земной поверхности в точке пересечения географического и геомагнитного экваторов планеты. По аналогии с расчетом Е для равномерно заряженного шара за пределами его объема будем полагать, что напряженность электрического поля у поверхности Земли (E_Z) в этом месте примерно равна:

 

 В / м,     (6)

 

где:  Q_Z » 5,7*10⁵ Кл – величина электрического заряда на поверхности Земли [1];

        R_Z = 6378140 м – экваториальный радиус нашей планеты [3];

        4pe₀ = 1,11265*10^-10 Кл² / Н * м²  (где: e₀ – электрическая постоянная).

____________________________________________________________

      

 

 

Пример 1: «Притяжение к поверхности Земли монолитного объекта из каменной соли»

 

Используя умозрительный прием, представим себе в качестве первого объекта кристалл каменной соли (хлорида натрия – NaCl) в виде монолитного куба единичного объема (1 м³).

 

Почему кристалл и такого объема? Все очень просто: во-первых, в кристаллическом состоянии вещество обнаруживает свои физические свойства в самом чистом виде и богатых сочетаниях, а во-вторых, единичный объем (1 м³) упростит вычисления.

 

Приравняем гравитационную силу F_G, с которой данный объект должен притягиваться к Земле, к его весу Р. Для покоящегося на земной поверхности тела (рис.5):  

P » m G,     (7)

 

где:  Р – вес тела, Н;  m – масса тела, кг;  G – напряженность гравитационного поля Земли, численно равная величине ускорения

                                                                           свободного падения (среднее значение в районе экватора на уровне моря примерно

                                                                           равно 9,78 м / с²), Н / кг.

 

 

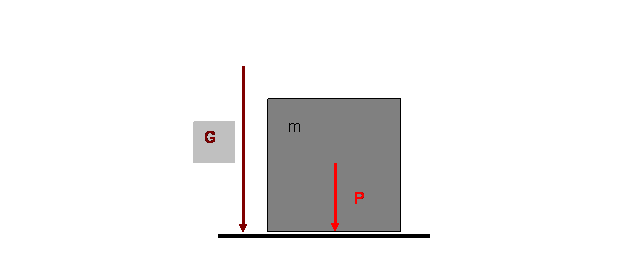
Рис.5

 

Плотность хлорида натрия r = 2173 кг / м³  [1]. Другими словами, масса m кристалла NaCl при его объеме в 1 м³ должна быть равной 2173 кг. Отсюда нетрудно вычислить вес Р данного тела:

 

Р » m G = 2,17*10³ * 9,78 = 2,12*10⁴ Н.     (8)

 

Обратимся теперь к внутренней структуре кристалла NaCl [4] и конфигурациям электронных оболочек атомов, из которых этот кристалл состоит. Необходимо будет определить суммарную величину заряда электронных оболочек поверхностных атомов рассматриваемого объекта.                                                                                                                      

 

В кристалле каменной соли атомы натрия (Na) и хлора (Cl) образуют пространственную решетку в виде правильной трехмерной кубической сетки (рис.6).

 

 

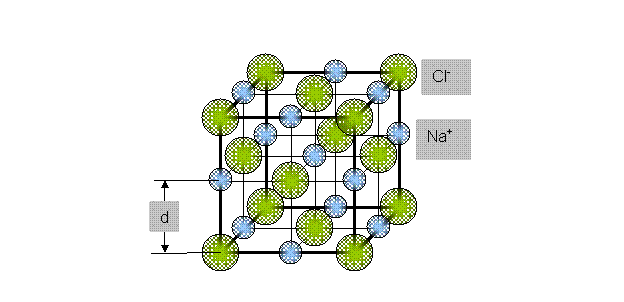
Рис.6  Элементарная ячейка кристалла каменной соли (NaCl)

 

 

Константа d на схеме - ближайшее расстояние между центрами двух соседних частиц в элементарной ячейке кристалла NaCl. Опытным путем установлено, что:

d = 2,79*10^-10 м.     (9)

 

Значит на поверхности такого кристалла площадью в 1 м² могут разместиться в один слой примерно N частиц:

 

N = (1 / d)² = (1 / 2,79*10^-10)² = 1,3*10¹⁹ частиц.     (10)

 

Поскольку атомы натрия и хлора в кристалле представлены поровну, то тех и других на поверхности одной грани (1 м²) монолитного куба каменной соли должно быть по N¢ частиц каждого вида:

 

N¢ = N / 2 = 1,3*10¹⁹ / 2 = 6,5*10¹⁸.     (11)

 

В отношении конфигураций электронов в оболочках атомов коротко можно пояснить следующее. Для удобства классификации электронов в атоме их условно разбивают на электронные слои (энергетические уровни) и подслои (энергетические подуровни). В подслое может быть несколько орбиталей (энергетических ячеек) с электронами.

 

В основу графического построения электронных формул кладут орбиталь, которую изображают в виде квадратика или прямоугольника, а электроны в ней - стрелками, направленными соответственно «спину». На одной орбитали могут находиться не более двух электронов, и то при условии, если они антипараллельны (принцип Паули – швейцарского физика).

 

 

Вольфганг Паули (1900 – 1958)

 

А теперь, на основе известных физико-химических сведений о хлориде натрия и в рамках  поставленной задачи, попробуем  вспомнить и понять - как из отдельно «взятых» нейтральных атомов Na и Cl может образоваться кристалл с должным поверхностным зарядом q^-. Конфигурации электронных оболочек отдельно взятых («изолированных») атомов натрия (Na) и хлора (Cl) даны на рис7.

 

 

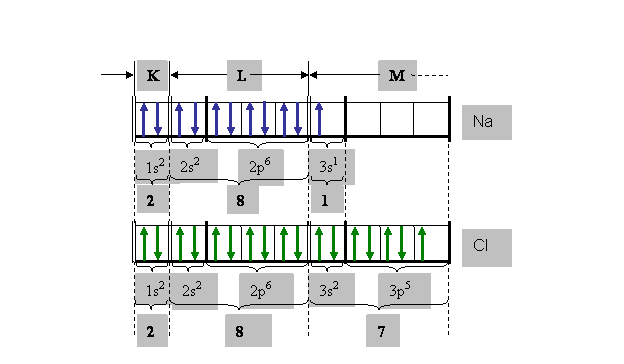
Рис.7  Графические формулы строения электронных оболочек отдельно взятых атомов натрия (Na) и хлора (Cl): 

                                   K, L, M, … – буквенное обозначение энергетических уровней;

                                   1, 2, 3, …– цифровое обозначение энергетических уровней;

                                   s, p, …– энергетические подуровни;

                                   1, 2, 7, 8, …– количество электронов на энергетических уровнях и подуровнях;

                                   цифровые индексы – количество электронов в слоях и подслоях.

 

При взаимодействии двух атомов-партнеров (допустим, при зарождении кристалла из атомов Na и Cl) атом хлора как бы «оттягивает» один электрон атома натрия с орбитали 3s¹ на себя, создавая связанную пару из ионов натрия (Na⁺) и хлора (Cl^–). Но при этом полного отторжения электрона от атома натрия не происходит (рис.8). Атом хлора способен оттянуть на себя согласно экспериментальным данным только 80% облака этого электрона (условно 0,8 заряда электрона).

 

 

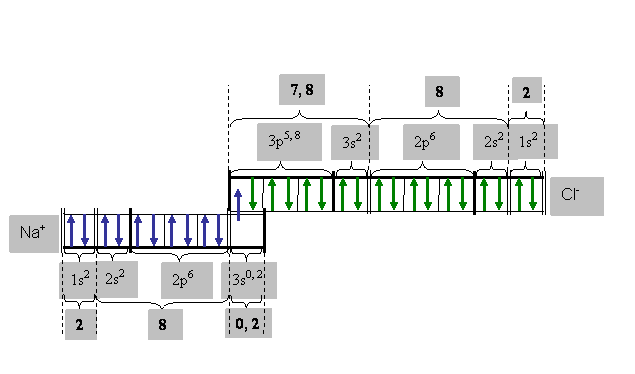
Рис.8  Возможная конфигурация электронов связанной пары ионов натрия (Na⁺) и хлора (Cl^-)

                                                   в поверхностном слое кристалла NaCl

 

Получается, что поверхностный атом натрия (Na) при образовании кристалла каменной соли как бы лишается 0,8 заряда электрона из внешнего слоя своей оболочки и превращается в ион Na⁺ с оставшимся электрическим зарядом оболочки (q _Na⁺), равным: 

 

q _Na⁺ = e (n – 0,8) = – 1,6*10^–19 (11 – 0,8) = – 1,6*10^–18 Кл,     (12)

 

где:  е = 1,6*10^-19 Кл – заряд электрона (элементарный электрический заряд);

        n = 11 – количество электронов в оболочке отдельно взятого атома натрия.

 

Соответственно, атом хлора (Cl) при этом как бы приобретает дополнительный заряд отрицательного знака в виде 0,8 электрона и становится ионом Cl^– c зарядом своей оболочки (q _Cl^–), равным:

 

q _Cl^– = e (n + 0,8) = – 1,6*10^–19 (17 + 0,8) = – 2,8*10^–18 Кл,     (13)

 

где: n = 17 – количество электронов в оболочке отдельно взятого атома хлора.

 

Поскольку на поверхности одной грани (1 м²) нашего кубического объекта находится N^/ ионов натрия, то их суммарный электронный заряд (S q _Na⁺) на этой площади составит:

 

S q _Na⁺ = q _Na⁺  *  N^/  = – 1,6*10^–18  * 6,5*10¹⁸  = – 10,4 Кл.     (14)

 

Ионы хлора, расположенные на этой же грани и в таком же количестве, будут иметь суммарный заряд своих оболочек (S q _Cl^–), равный:

 

S q _Cl^– = q _Cl^–  *  N^/  = –2,8*10^–18  * 6,5*10¹⁸  = – 18,2 Кл.     (15)

 

Общий электронный заряд оболочек ионов натрия и хлора (q _{Na – Cl}) на поверхности одной грани куба каменной соли примерно равен:

 

q _{Na – Cl} = (S q _Na⁺) + (S q _Cl^–) = (– 10,4) + (– 18,2) = – 28,6 Кл.     (16)

 

Примечание 1:  эта величина может считаться примерным показателем поверхностной плотности электронного заряда кристалла каменной соли (s _NaCl), то есть:

s _NaCl » – 28,6 Кл / м²     (17)

 

В результате электронный заряд (q) поверхности всех шести граней (k = 6) уcловного кристалла NaCl кубической формы (1 м³) получается равным:

q = q _{Na – Cl}  *  k = – 28,6 * 6 = –  171,6 Кл.     (17)

 

Примечание 2:  этого заряда «опасаться» не следует. Он всего лишь соответствует суммарному значению атомных токов натрия и хлора на поверхности кристалла NaCl площадью в 6 м² за период времени порядка 10^–14 с и является просто условно-расчетной величиной. Реальная же сила этих токов в кристалле примерно равна 10^–4 ампер, а человек начинает ощущать ток с величины 10^–3 А (пороговая реакция). Так что, употребляя поваренную соль, можно смело сочетать приятное (вкусовое раздражение) с полезным (подзарядкой  своих  телесных  клеток  током  супервысокой  частоты). В меру, конечно.

 

Все эти долгие рассуждения относительно поверхностного заряда (q) кубометра каменной соли укладываются в простую формулу:

 

 Кл,     (18)

 

где:  e = – 1,6*10^-19 Кл – заряд электрона;

        n _Na = 11 – количество электронов в оболочке отдельно взятого атома натрия;

        n _Cl = 17 – количество электронов в оболочке отдельно взятого атома хлора;

        N = (1 / d)² = 1,3*10¹⁹ – общее число атомов натрия и хлора в поверхностном слое кристалла NaCl площадью в 1 м²;

        k = 6 – количество граней куба.

 

В итоге электростатическая сила (F_E) притяжения к Земле монолитного кубометра каменной соли получается равной:

 

F_E = q E = – 1,7*10²  * 1,26*10²  = – 2,1*10⁴ Н.     (19)

 

Как видим, полученные значения сил (P = 2,12*10⁴ и F_E = – 2,1*10⁴ Н) находятся друг с другом в согласии. Знак «минус» у результата вычисленной силы F_E указывает на то, что она является силой притяжения (так принято в электростатике), а не отталкивания.

 

Таким образом, уже появляется некоторое основание считать, что рациональное зерно в предложенной гипотезе присутствует. Но полученный результат, естественно, требует подтверждения своей закономерности. Поэтому сделаем теперь соответствующие вычисления применительно к веществу, состоящему из атомов одного «сорта», например, к алюминию.

________________________________________________________________________________________

          

 

 

Пример 2: «Притяжение к земной поверхности объекта из алюминия»

 

Кристалл алюминия (Al) имеет кубическую плотнейшую гранецентрированную решетку (рис.9). Если плотность его r = 2710 кг / м³, то вес (Р) этого металла кубической формы и единичного объема на уровне моря в районе экватора должен быть равным:

 

P » m G = 2,71*10³ * 9,78 = 2,65*10⁴ Н.     (20)

 

 

Рис.9

 

 

Отдельно взятый атом алюминия содержит в своей оболочке три валентных электрона. При зарождении кристалла два таких возбужденных атома (Al₁ и Al₂), очевидно, могут объединить распаренные электроны в дублеты, достраивая свои подуровни тремя привлеченными электронами из оболочки атома-партнера (рис.10). В этом случае взаимодействующий атом, оттягивая на себя электроны из оболочки партнера, скорее всего может «расчитывать» только на половину их электрического заряда, так как  здесь в образовании связанной пары участвуют уже равноправные партнеры (атомы одного сорта). Таким образом, будем полагать, что каждый поверхностный атом кристалла алюминия получает в процессе взаимодействия от трех привлеченных электронов партнера дополнительный заряд, как бы эквивалентный заряду полутора электронов.

 

 

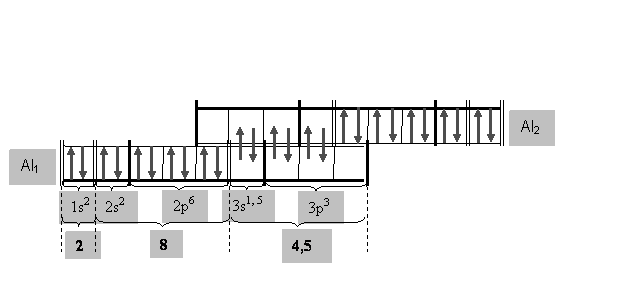
Рис. 10  Возможная конфигурация электронов связанной пары атомов в поверхностном слое кристалла алюминия

 

Тогда общий электрический заряд (q) электронных оболочек поверхностных атомов условного монолитного кристалла Al кубической формы и единичного объема должен приблизительно составить:

 

q = [e (n + 1,5) N] k = – 2,1*10² Кл,     (21)

 

где:  е = – 1,6*10^-19 Кл – заряд электрона;

        n = 13 – количество электронов в оболочке отдельно взятого атома алюминия;

 

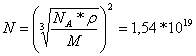         – количество атомов алюминия в поверхностном слое его кристалла на площади 1 м²,

 

                                         где:  N_A = 6,022*10²⁶ кмоль^-1 – число Авогадро;

                                                 r = 2710 кг / м³ – плотность алюминия в данном примере;

                                                 М = 26,98 – относительная атомная масса алюминия;

                                                 k = 6 – число граней алюминиевого куба.

 

В таком случае сила (F_E) электростатического притяжения алюминиевого монокристалла кубической формы и единичного объема к Земле на уровне моря в районе экватора получается равной:

 

F_E = q E = – 2,1*10² * 1,26*10² = – 2,65*10⁴ Н.     (22)

 

Результат этого примера (P = 2,65*10⁴ Н и F_E = – 2,65*10⁴ Н) также обнадеживает. Но ведь кроме твердых кристаллических веществ в природе существуют еще и жидкости. Поэтому, в завершение «электростатической» части разговора на тему гравитации рассмотрим пример с обыкновенной водой.

___________________________

            

 

 

Пример 3: «Притяжение к Земле водной массы»

 

Представим себе емкость в виде куба с внутренним объемом в 1 м³. Наполним ее доверху водой, плотность которой r = 1000 кг / м³. Вес (Р) кубометра этой воды у поверхности Земли в районе экватора будет примерно равен:

 

P » m G = 1*10³ * 9,78 = 9,8*10³ Н.     (23)

 

А теперь вес (Р) данного объема воды выразим через силу (F_E) его электростатического притяжения к земной поверхности. Несмотря на то, что вода и, скажем, алюминий различаются по своим физическим свойствам весьма значительно, общий подход к решению поставленной задачи останется прежним. Ведь вода в облике ледяного куба – тоже кристалл. Кстати, слово «кристалл» произошло от греческого krystallos и во времена Гомера (XII – VII вв. до н. э.) означало «лед». Но в отличие от металлической пространственной решетки алюминия структурной единицей воды считается ее молекула (Н₂О). И расчет здесь, очевидно, нужно строить через электронный заряд этой молекулы (рис.11).

 

 

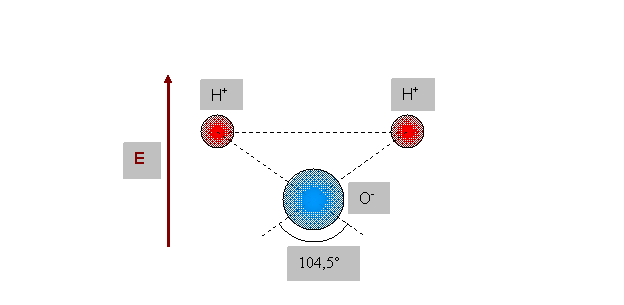
Рис.11  Схема молекулы воды (Н₂О)

 

 

Попробуем осилить данную задачу, используя некоторые положения теории молекулярных орбиталей (ТМО). В ТМО принимается, что при образовании молекул из атомов происходит обобществление атомных электронов. Путем взаимного наложения (перекрывания) облаков последних возникает комбинация новых облаков, уже общих для всей молекулы в целом. Это молекулярные орбитали. Такова вкратце основная суть этой теории.

 

Как известно, отдельные атомы водорода (Н) и кислорода (О), предоставленные самим себе, группируются парами в молекулы газов Н₂ и О₂. Из ТМО следует, что молекула Н₂ имеет на молекулярной орбитали 2 электрона, а в молекуле О₂ на ней находятся 12 электронов.

 

При объединении молекул Н₂ и О₂ в изобарном процессе (р = const) получается вода:

 

2 Н₂  +  О₂  ®  2 Н₂О.     (24)

 

Определим количество молекулярных электронов, приходящихся на одну молекулу Н₂О по принципу аддитивности, то есть:

 

 2 Н₂          +            О₂              ®            2 Н₂О             

                                                                          (4 электрона)       (12 электронов)        (16 электронов)

 

Таким образом, если две молекулы воды располагают 16 молекулярными электронами, то на одну молекулу Н₂О будет приходиться n = 8 таких электронов. Вычислим электронный заряд (q ^/ ) молекулы воды:

 

q ^/ = e * n = – 1,6*10^–19  *  8 = – 1,3*10^–18 Кл.     (25)

 

где:  е = – 1,6*10^-19 Кл – заряд электрона.

 

Количество (N) молекул, образующих поверхностный слой водяного (ледяного) куба единичного объема, можно определить через объем (V) одной молекулы:

 

 м³,     (26)

 

где:  М = 18,02 – относительная молекулярная масса Н₂О;  N_A = 6,02*10²⁶ кмоль^-1 – число Авогадро;  r = 1*10³ кг / м³ – плотность воды.

 

Отсюда:

 молекул.     (27)

 

где:  k = 6 – количество граней куба.

 

Электронный заряд (q) поверхностных молекул кубометра воды примерно равен:

 

q = q ^/  *  N = – 1,3*10^–18  *  6*10¹⁹  = – 78 Кл     (28)

 

Тогда сила (F_E) электростатического притяжения данного объема воды к земной поверхности получается равной:

 

F_E = q E = – 0,78*10²  * 1,26*10²  = – 9,83*10³ Н.     (29)

 

Как видим, принятая к исследованию гипотеза не подвела и здесь. Разница значений P = 9,8*10³ Н и F_E = – 9,83*10³ Н в этом примере находится в разумных пределах.

 

Итак, отметим, что результаты трех простых примеров в отношении сущности механизма гравитации, рассмотренные через призму электростатики, вышеизложенную гипотезу не отвергают. В таком случае, если данная гипотеза действительно отражает объективную реальность, то и в рамках понятий о магнетизме мы должны получить в подобных примерах  идентичные или близкие к ним результаты.

____________________________________________________________